Wizualizacja problemów z metodą naiwną
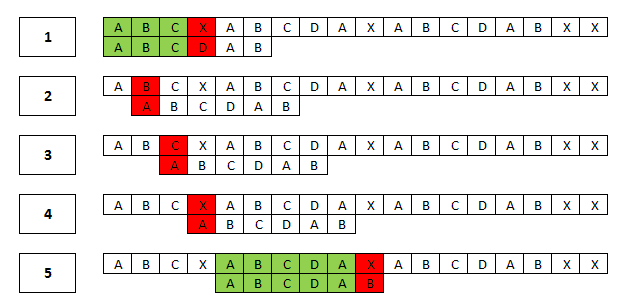
W pierwszym kroku znaleźliśmy trzy kolejne pasujące znaki i dopiero na pozycji czwartej natrafiliśmy na pierwsze niedopasowanie. Wiemy, że nasze trzy pierwsze znaki są różne, a ponieważ pasowały do trzech pierwszych znaków tekstu przeszukiwanego, to z tego faktu możemy wyprowadzić wniosek, że dla przesunięcia równego o jeden oraz dwa znaki, nie uda nam się dopasować wzorca, jednakże – pomimo takiej obserwacji – metoda naiwna i tak stara się go dopasować (krok 2, 3).
Przedstawię, jak wstępnie przetworzyć wzorzec, tak aby poznać jego strukturę (samo podobieństwo) i dzięki temu być w stanie w pewnych sytuacjach zwiększyć przesunięcie o więcej niż jedno pole. Pokażę algorytm, który wykorzysta cechy wzorca i będzie zdolny do przejścia z kroku 1 bezpośrednio do kroku 5.
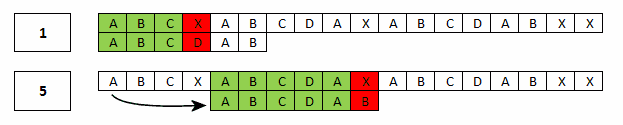
Oczywiście, jeśli we wzorcu znajdują się powtórzenia (prefikso-sufiks), to dopasowujemy wzorzec zgodnie z najdłuższym możliwym prefikso-sufiksem.

Wizualizacja oraz właściwości prefikso-sufiksu
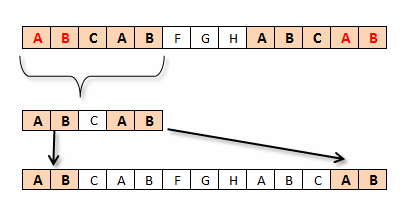
Prefikso-sufiksy dla różnych podciągów wzorca.

Aby efektywnie wyliczyć prefikso-sufiksu przy pomocy technik programowania dynamicznego, powinniśmy znać dwie jego właściwości:
- rozszerzalność prefikso-sufiksu,
- redukcja prefikso-sufiksu.
Rozszerzalność prefikso-sufiksu
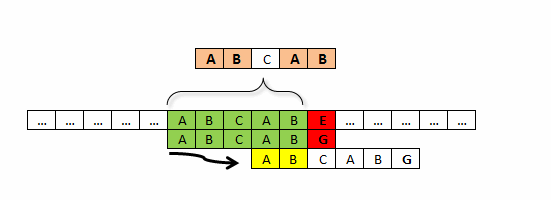
Jeśli do łańcucha tekstowego S o długości N, który posiada prefikso-sufiks o długości K, dodamy kolejny znak, to jeśli nowy znak będzie identyczny ze znakiem S[k]. Wówczas najdłuższy prefikso-sufiks nowego łańcucha tekstowego będzie miał długość K+1.

Redukcja prefikso-sufiksu
Jeśli łańcuch S posiada prefikso-sufiks PS1 oraz PS1, posiada swój własny prefikso-sufiks PS2. Wówczas PS2 jest również prefikso-sufiksem łańcucha S.
Jeśli PS1 jest maksymalnym prefikso-sufiksem S, oraz PS2 jest maksymalnym prefikso-sufiksem PS1, to wówczas nie istnieje żaden prefikso-sufiks S dłuższy niż PS2 inny niż PS1.
Implementacja algorytmu Morrisa-Pratta
Przekształcenie wzorca
Dla każdego prefikso-sufiksu dokonujemy sprawdzenia prefikso-sufiksu o jeden mniejszego i próbujemy go rozszerzyć. Jeśli rozszerzenie poprzedniego prefikso-sufiksu się nie udało, to szukamy kandydata wśród kolejnych zagnieżdżonych prefikso-sufiksów.
def TransformPattern_MorrissPratta(pattern):
MPNext_size = len(pattern) + 1
MPNext = [0] * MPNext_size
pos = MPNext[0] = -1
for i in range(1, MPNext_size):
while pos > -1 and pattern[pos] != pattern[i - 1]:
pos = MPNext[pos]
pos += 1
MPNext[i] = pos
return MPNextPrzykładowe wyniki przekształcenia wzorca wg algorytmu Morrisa-Pratta
pattern: ABCWERABCT
A B C W E R A B C T
-1 0 0 0 0 0 0 1 2 3 0
pattern: AAAAAAAAA
A A A A A A A A A
-1 0 1 2 3 4 5 6 7 8
pattern: ABCABCABC
A B C A B C A B C
-1 0 0 0 1 2 3 4 5 6
pattern: RFDVTBPOMSFVTB
R F D V T B P O M S F V T B
-1 0 0 0 0 0 0 0 0 0 0 0 0 0 0Wyszukiwanie wzorca wg algorytmu Morrisa-Pratta
def find_MorrissPratta(s,pattern,MPNext):
b = 0
for i, char_S in enumerate(s):
while b > -1 and pattern[b] != char_S:
b = MPNext[b]
b += 1
if b == len(pattern):
return i-len(pattern)+1
return -1Jeśli podczas próby dopasowania wzorca natrafimy na niedopasowanie, to możemy przesunąć wzorzec nie o jedno pole jak w algorytmie naiwnym, ale o całą długość dopasowanej cześci wzorca pomniejszonej o długość najdłuższego prefikso-sufiksu. Dzięki temu usprawnieniu pomijamy pewne niepotrzebne porównania.
Algorytm Knuth-Morris-Pratt
Sam algorytm Morris-Pratt wprowadza znaczne zwiększenie wydajności w stosunku do podejścia naiwnego, jednak Donald Knuth odkrył, jak można jeszcze bardziej ulepszyć ten algorytm – tak powstał Algorytm Knuth-Morris-Pratt, nazywany również algorytmem KMP. Samo wyszukiwanie jest identyczne, jak w metodzie MP, różnica jest dostrzegamy jedynie w sposobie przetworzenia wzorca. W Metodzie KMP wyznaczamy tablice KMPNext zamiast MPNext.
Ulepszenie wprowadzone przez Donalda Knutha pozwalało zmniejszyć ilość przypadków, kiedy po przesunięciu nieudanego dopasowania częściowego mieliśmy różnicę znaków już przy pierwszym nowym porównaniu.
Rozważmy teraz następujący przypadek:
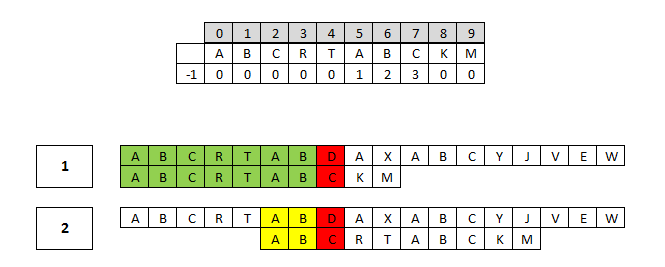
Zgodnie z podejściem MP przesuwamy wzorzec i natychmiast natrafiamy na niedopasowanie za pierwszym porównaniem. W tym miejscu algorytm KMP wprowadza ulepszenie – korzysta on z faktu, że to niedopasowanie możemy przewidzieć z samej struktury wzorca. Po wystąpieniu ciągu “AB” kolejny znak “C” jest taki sam jak trzeci znak w ciągu “C”, więc za każdym razem, gdy znajdziemy niedopasowanie na pozycji siódmej, możemy przesunąć wzorzec o całe siedem pozycji, a nie tylko o pięć jak w algorytmie MP.
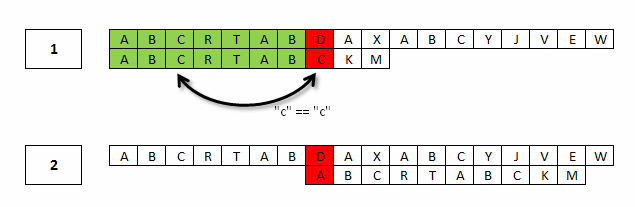
Algorytm obliczania tablicy KMPNext sprawdza, czy następny znak po sufiksie jest różny od znaku następującego po prefiksie. Jeśli znaki są różne, to wstawiamy do tabeli -1, co optymalizuje nam algorytm.
Porównanie tablicy KMPNext oraz MPNext
pattern: ABCWERABCT
A B C W E R A B C T
MP -1 0 0 0 0 0 0 1 2 3 0
KMP -1 0 0 0 0 0 -1 0 0 3 0
pattern: AAAAAAAAA
A A A A A A A A A
MP -1 0 1 2 3 4 5 6 7 8
KMP -1 -1 -1 -1 -1 -1 -1 -1 -1 8
pattern: ABCABCABC
A B C A B C A B C
MP -1 0 0 0 1 2 3 4 5 6
KMP -1 0 0 -1 0 0 -1 0 0 6
pattern: RFDVTBPOMSFVTB
R F D V T B P O M S F V T B
MP -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
KMP -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0Implementacja Algorytmu KMP
Wyszukiwanie wzorca jest zaimplementowane identycznie jak w przypadku algorytmu MP, jedynie korzysta z innej tablicy przesunięć.
Samo wyznaczanie tablicy przesunięć różni się tylko jednym dodatkowym warunkiem w stosunku do algorytmu MP.
def TransformPattern_KMP(pattern):
KMPNext_size = len(pattern) + 1
KMPNext = [0] * KMPNext_size
pos = KMPNext[0] = -1
for i in range(1, KMPNext_size):
while pos > -1 and pattern[pos] != pattern[i - 1]:
pos = KMPNext[pos]
pos += 1
if i == KMPNext_size-1 or pattern[i] != pattern[pos]:
KMPNext[i] = pos
else:
KMPNext[i] = KMPNext[pos]
return KMPNext
def find_KMP(s,pattern):
KMPNext = TransformPattern_KMP(pattern)
b = 0
for i, char_S in enumerate(s):
while b > -1 and pattern[b] != char_S:
b = KMPNext[b]
b += 1
if b == len(pattern):
return i-len(pattern)+1
return -1