Analiza danych jest jak obieranie cebuli, warstwa po warstwie.
Obserwacje, które są prawdziwe dla każdej grupy z osobna, mogą przestać być prawdziwe dla populacji bez podziału na grupy.
Na dane musisz patrzeć jednocześnie z bliska i z daleka.
Paradoks Simpsona, a efekt perspektywy
Wyobraźmy sobie sklep z ciastkami, w ofercie mamy dwa rodzaje ciastek jabłkowe i wiśniowe. Właściciel sklepu przeprowadził badania popularności i zatrudnił nas, aby przeprowadzić analizę zebranych wyników.
Badanie opinii klientów sklepu
Aby zebrać opinie o preferencjach swoich klientów, przez kilka dni ankieterzy podchodzili do przechodniów przed sklepem, oferowali im ciastko w zamian za wypełnienie ankiety. Ankieta zawierała główne pytanie: "Czy ciastko było smaczne" oraz kilka pytań o płci, wieku i statusu osoby testowanej. Zebrano następujące wyniki:
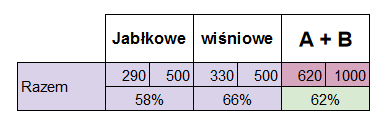
Patrzymy na dane z daleka
Jakie informacje możemy wyczytać z tak przedstawionych danych?:
- Przetestowano 1000 osób.
- Ciastko wiśniowe jest smaczne dla 66% respondentów, co jest o 8 p.p. więcej niż w przypadku ciastka jabłkowego
- Rozdano tyle samo ciastek o poszczególnym typie.
- Dla 62% respondentów ciastko okazało się smaczne.
Czy to oznacza, że ciastka wiśniowe są smaczniejsze? Czy gdyby firma mogła produkować tylko jeden rodzaj produktu, to powinna wybrać ciastko wiśniowe?
Jeden poziom głębiej podział na dwie grupy wg. płci
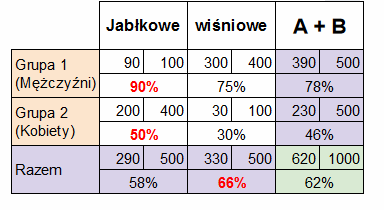
Jakie informacje możemy wyczytać z tak przedstawionych danych?:
- W grupie kobiet wierszą sympatią cieszą się ciastka jabłkowe.
- W grupie mężczyzn również większą sympatią cieszą się ciastka jabłkowe.
- Mężczyźni są grupą klientów, która jest bardziej tolerancyjna i za smaczne uzna więcej ciastek niż kobiety.
- Obie grupy są jednakowo liczne.
- Struktura testów w grupach jest znacząco inna niż w populacji.
- Proporcje testowanych ciastek w poszczególnych grupach są bardzo różne.
Czy mając takie dane, możemy stwierdzić, które ciastka są preferowane przez klientów? A co jeśli przedstawimy tylko wynik procentowy w grupach bez wartości bezwzględnych?
| Jabłkowe | Wiśniowe | |
|---|---|---|
| Mężczyźni | 90% | 75% |
| Kobiety | 50% | 30% |
Uwaga
Czy takie przedstawienie danych to nadal wizualizacja czy już manipulacja danymi?
Inny podział wg. wieku
Tych samych ankietowanych możemy podzielić wg. wieku:
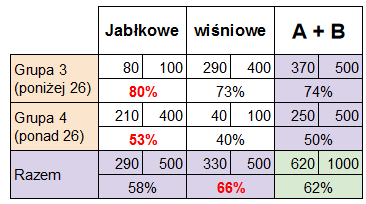
Widzimy, że:
- Grupy są równo liczne, ale mają bardzo różną strukturę.
- Obserwacje prawdziwe dla każdej z grup przestają byż prawdziwe dla całej populacji.
Paradoks Simpsona - Podsumowanie
Kluczowe w prezentowanych przykładach jest to, że preferencje ciastko A lub B się wzajemnie nie wykluczają. Osoby, które określiły dane ciastko jako smaczne, mogą inne ciastko również określić jako smaczne.
Kolejna sprawa to czy zaoferowanie ciastko było całkowicie przypadkowe, czy była tam ukryta korelacja z grupą? Można wyobrazić sobie wiele czynników zakłócających.
Widzimy, ż pewne efekty występują w grupach, ale giną lub wręcz zmieniają zwrot, gdy patrzymy na całą populację. To dlatego tak pożądane jest właściwe przypisywanie klienta do grupy, aby sprawniej optymalizować dla nich produkty.