Programowanie dynamiczne #2

Zadanie – Longest Common Subsequence

Mamy dwa ciągi znaków, znajdź najdłuższa możliwą sekwencje znaków (niekoniecznie kolejnych), występującą w obydwu ciągach.
Przykład:

A = ABRSFBORGSNIDFMSOAFBGNETGRIFNIREYJNBSDF
B = UKRYTRIFNIREYJNBSTHDBRHFDHMD

Wynik: RTRIFNIREYJNBSDF

Rozwiązanie – programowanie dynamiczne

Algorytm

Przyjrzyjmy się uproszczonemu przypadkowi.

Czy wiedząc, że najdłuższym wspólnym podciągiem dla “abc” oraz “acc” jest “ac”, możemy jakoś wykorzystać tę informację i stwierdzić, jaki będzie najdłuższy wspólny podciąg, gdy dopiszemy jedną literkę do pierwszego ciągu? Na samym początku przedstawmy naszą wiedzę w tabeli. Wartości w komórkach przedstawiają długość najdłuższego wspólnego podciągu. Możemy stwierdzić, że najdłuższy wspólny podciąg będzie zawsze mniejszy lub równy krótszemu z argumentów. Dzięki tej informacji możemy wypełnić pierwszą kolumnę i pierwszy wiersz zerami.

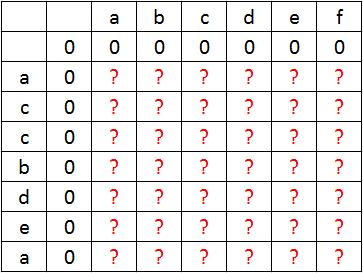
Pierwsze znaki w obu ciągach to “a”, więc dla komórki (1,1) mamy maksymalną długość 1.

Widzimy, że skoro pierwsze znaki pasują do siebie, to bez względu na kolejne wartości tak długo, jak jeden z argumentów będzie miał długość 1, to maksymalna długość wspólnego podciągu również będzie jeden. Wypełniliśmy pierwszy rząd i pierwszą kolumnę.

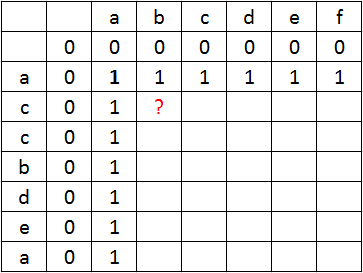
Teraz do naszych dwóch jednoznakowych ciągów dopisujemy po jednej literce. Jaka będzie LCS dla {“ac“, “ab“}? Czy możemy wykorzystać naszą tabelkę, aby odpowiedzieć na to pytanie?

Dodane literki są różne, więc nie mogą wydłużyć naszego zaczętego przez pierwsze znaki ciągu, natomiast nie są one również zdolne do pogorszenia obecnej sytuacji. W obecnym momencie:

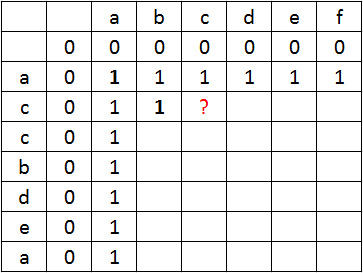
Ile wynosi ? Dokładamy jeden znak w taki sposób, by ostatnie znaki były identyczne, a zatem ostatnie znaki z obu argumentów były częścią naszego wspólnego ciągu.

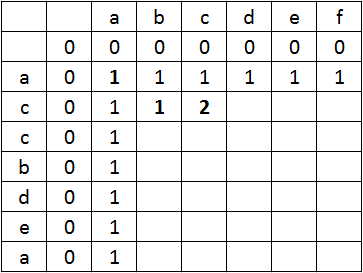
Możemy teraz napisać formułę matematyczną określającą maksymalną długość LCS.

Wykorzystując otrzymaną zależność, wypełniamy naszą tabelę.

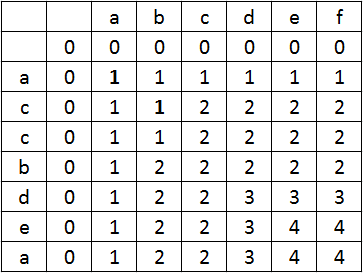
Widzimy, że LCS ma długość 4. Aby poznać wartość tego ciągu, musimy określić drogę, która prowadziła do ostatniego pola. Dla pokazanego zestawu danych kilka różnych ciągów może spełniać warunek najdłuższego.

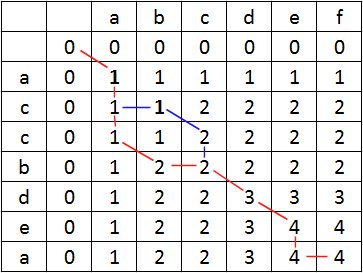
Kod demo Python 3

A = "ABRSFBORGSNIDFMSOAFBGNETGRIFNIREYJNBSDF"
B = "UKRYTRIFNIREYJNBSTHDBRHFDHMD"

db = [[0 for b in range(len(B)+1)] for a in range(len(A)+1)]

for a in range(len(A)):
    prev_row = db[a]
    curr_row = db[a+1]
    a_char = A[a]
    for b in range(len(B)):
        b_char = B[b]
        if a_char == b_char:
            curr_row[b+1] = prev_row[b]+1
            continue
        curr_row[b+1] = max(curr_row[b], prev_row[b+1])

a = len(A)
b = len(B)
wynik = []

while a > 0 and b > 0:
    a_char = A[a-1]
    b_char = B[b-1]
    if a_char == b_char:
        a -= 1
        b -= 1
        wynik.append(a_char)
        continue
    if db[a-1][b] > db[a][b-1]:
        a -= 1
        continue
    b -= 1

print ("".join([str(a) for a in wynik[::-1]]))

Kod demo C++

#include <iostream>

using namespace std;

char A[] = "ABRSFBORGSNIDFMSOAFBGNETGRIFNIREYJNBSDF";
char B[] = "UKRYTRIFNIREYJNBSTHDBRHFDHMD";

constexpr int lenA = sizeof(A) / sizeof(A[0]);
constexpr int lenB = sizeof(B) / sizeof(B[0]);

int main() {
    auto C = new int[lenA+1][lenB+1]();  //c++11

    for ( int a=0; a < lenA; ++a ) {
        char a_char = A[a];

        for (int b = 0; b < lenB; ++b) {
            char b_char = B[b];
            if (a_char == b_char) {
                C[a+1][b+1] = C[a][b]+1;
                continue;
            }
            C[a+1][b+1] = max(C[a+1][b], C[a][b+1]);
        }
    }

    int a = lenA;
    int b = lenB;
    string buf;

    while (a > 0 and b > 0) {
        char a_char = A[a - 1];
        char b_char = B[b - 1];
        if (a_char == b_char) {
            a --;
            b --;
            buf.append(&a_char,1);
            continue;
        }
        if (C[a - 1][b] > C[a][b - 1]) {
            a --;
            continue;
        }
        b --;
    }

    string wynik(buf.rbegin(), buf.rend());
    cout << wynik << endl;


    return 0;
}

Dyskusja złożoności

Tablica C zawiera n*m elementów. Wyliczenie wartości elementu tabeli C wymaga inspekcji nie więcej niż trzech innych elementów tej tablicy. Tak więc mamy złożoność obliczeniową O(m*n). Rekonstrukcja ciągu wymaga nie więcej niż O(m+n) operacji. Finalna złożoność obliczeniowa to O(m*n).

Pamięciowo potrzebujemy M(m*n) elementów tabeli C.

Wytłumaczenie Video

Odnośniki

• Geeks for geeks – Dynamic Programming (opens new window)