Treść zadania
Mamy dany ciąg liczb, reprezentujący wysokość terenu, należy znaleźć głębokość największego wąwozu.
Przykłady
| Dane | Wynik |
|---|---|
| 1, 2, 3 | NONE |
| 5, 1, 5 | 4 |
| 9, 4, 6 | 2 |
| 5, 4, 3, 7, 2, 9, 9, 5, 4, 3, 0, 8, 4 | 8 |
Ilustracja graficzna
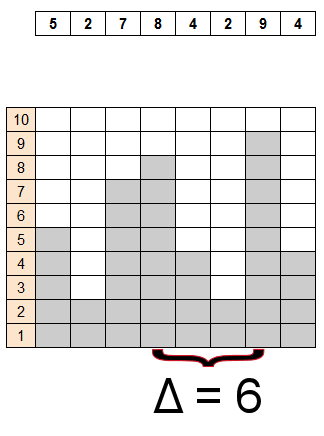
Rozwiązanie
Kod dostępny na GitHub (opens new window)
class DeepestDitch:
def __init__(self, data):
self._values = [None, None, None]
self._deep = None
if len(data) < 3:
return
candidates = [data[0], None]
for i, value in enumerate(data):
if self._values[2] is not None and value > self._values[2]:
self._values[2] = value
self._deep = self._compute_deep(self._values)
if value > candidates[0] and candidates[1] is None:
candidates[0] = value
continue
if value < candidates[0] and (candidates[1] is None or value < candidates[1]):
candidates[1] = value
continue
if candidates[1] is not None and value > candidates[1]:
temp_depth = self._compute_deep([*candidates, value])
if self._deep is None or temp_depth > self._deep:
self._values = [*candidates, value]
self._deep = temp_depth
candidates = self._get_candidates()
continue
if value > candidates[0]:
candidates = self._get_candidates()
if any([a is None for a in self._values]):
return
self._deep = self._compute_deep(self._values)
@staticmethod
def _compute_deep(values):
deltas = [values[a] - values[1] for a in (0, 2)]
return min(deltas)
def _get_candidates(self):
if self._values[2] > self._values[0]:
return [self._values[2], None]
return [self._values[0], self._values[1]]
def get_depth(self):
return self._deep
def deepest_ditch(data):
deepest_ditch_obj = DeepestDitch(data)
return deepest_ditch_obj.get_depth()Omówienie rozwiązania
Zadanie zostało rozwiązane przy pomocy techniki programowania dynamicznego. Każda mowa wartość pozwala ulepszyć istniejące rozwiązanie lub jest zapamiętywana jako element lepszego rozwiązania, które może się pojawić w przyszłości.
Złożoność
- Złożoność czasowa - Liniowa
- Złożoność pamięciowa - Stała